Графы специального вида
Приведем примеры некоторых графов специального вида.
 |
Граф G называется полным, если любые две его вершины смежны, т.е.
E(G) = (V(G))(2). Полный граф порядка п обозначается символом Кп, в нем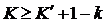
ребер. На рис. 2.5 изображены графы Кп, 
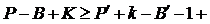. Граф называется пустым, если в нем нет ребер. Пустой граф порядка п обозначается Оп.
Красивыми примерами являются графы пяти платоновых тел (т.е. правильных многогранников): тетраэдра, куба, октаэдра, додекаэдра, икосаэдра (рис. 2.6).
Ниже неоднократно используются термины “разбиение” и “покрытие”. Набор подмножеств множества S называется покрытием множества S, если объединение этих множеств совпадает с S. Покрытие называется разбиением, если никакие два из входящих в него множеств не пересекаются.
 |
Граф называется двудольным, если существует такое разбиение множества его вершин на две части (доли), что концы каждого ребра принадлежат разным частям. Если при этом любые две вершины, входящие в разные доли, смежны, то граф называется полным двудольным. Полный двудольный граф, доли которого состоят из p и из q вершин обозначается символом 
при р = 1 получаем звезду 
. На рис. 2.7 изображены звезда 
и полный двудольный граф 
.
Заметим, что одна из долей двудольного графа может быть пустой. Так, О1 – двудольный граф с одной пустой долей, О2 можно трактовать как двудольный граф с двумя одновершинными долями или как двудольный граф, одна из долей которого содержит две вершины, а другая является пустым множеством.