Функции двух переменных
В таблице 1.6 представлены все булевы функции от двух переменных.
Табл. 1.6
 |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Функция называется конъюнкцией и , обозначается & или 
, или 
, и часто читается « и ».
Функция называется суммой по модулю 2 и , обозначается 
или 
, и часто читается « плюс ».
Функция называется дизъюнкцией и , обозначается 
, и часто читается « или ».
Функция называется стрелкой Пирса и , обозначается 
, и часто читается «ни , ни » или «ни и ни ». В технической литературе ее обычно называют антидизъюнкцией или функцией Вебба (а также функцией Даггера).
Функция называется эквиваленцией (или эквивалентностью) и , обозначается 
или 
, или 
, и читается « эквивалентно ».
Функция называется импликацией и , обозначается 
или 
, и часто читается « имплицирует » или «из следует ».
Функция называется штрихом Шеффера и , обозначается 
и часто читается «не или не » или « и не совместны». В технической литературе ее обычно называют антиконъюнкцией.
Символы из множества 
, в алгебре логики участвующие в обозначениях элементарных функций, называют логическими связками. Задачи для самостоятельного решения
1. Найти номера следующих двоичных наборов:
а) (1010); б) (1001001);
в) (0011001110); г) 
;
д) 
;
е) 
.
2. Найти двоичный набор длины 
, являющийся разложением числа 
:
а) 
; б) 
;
в) 
;
;
г) 
.
3. Для сравнимых наборов множества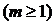 
из 
выписать их в порядке предшествования (
).
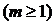соседние и противоположные наборы, и, если они имеются, выписать их: а) 
{(001), (010), (101), (100), (110), (111)};
б){(00111), (01011), (00110), (10110), (11010), (01010), (11100), (11011)}.
4. Найти:
а) число наборов 
из , имеющих вес (
);
б) число наборов из , удовлетворяющих условию 
(
);
в) число упорядоченных пар соседних наборов в ();
г) число упорядоченных пар 
наборов из , таких, что 
(
);
д) число наборов из веса , у которых между любыми единичными компонентами находится не менее 
нулевых компонент (
).
5.
Показать, что:а) два различных набора в , имеющих одинаковый нес, несравнимы;
б) в существуют только два сравнимых противоположных набора;
в) всякое подмножество наборов в , содержащее не менее 
наборов, содержит пару несравнимых наборов (
);
г) число наборов в , не сравнимых с фиксированным набором , имеющим вес , равно 
().
6. Найти число функций в 
, удовлетворяющих условию:
а) на данных наборах значения функции фиксированы, а на остальных произвольные (
);
б) на противоположных наборах функция принимает одинаковые значения ();
в) на каждой паре соседних наборов функция принимает противоположные значения ();
г) функция равна 0 не менее чем на половине наборов ().
7. а) На аварийном пульте системы расположены четыре сигнальные лампочки 
. Система выключается в случае, когда выполняется хотя бы одно из следующих условий: а) загорелась лампочка 
, но не загорелась лампочка 
; б) загорелись лампочки и 
, но не загорелась лампочка 
; в) загорелась лампочка и не горит лампочка .
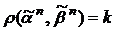булевой функции 
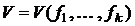, характеризующей условия выключения системы, т.е. 
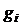тогда и только тогда, когда справедливо хотя бы одно из условий а), б), в); при этом предполагается, что 
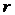, если лампочка 
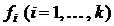горит, и 
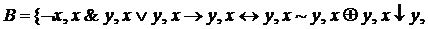, если лампочка 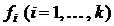не горит. б) Четырем членам 
некоторой комиссии сформулированы следующие условия посещения заседаний (хотя бы одно из них они должны выполнить): а) в заседании не участвует ни 
, ни 
, но должен быть 
; б) в заседании принимают участие и 
, но отсутствует ; в) на заседании должны присутствовать и . Обязан ли присутствовать на заседании член , если в нем не участвует ?
8. Указать все фиктивные переменные у функции 
:
а) 
;
б) 
;
в) 
.
9. Через 
обозначим множество всех булевых функций , зависящих от переменных 
и притом от каждой из них существенным образом.
а) Выписать все функции множества 
.
б) Найти число элементов множества 
.
в) Доказать, что число элементов множества равно 
. Ответы
1. а) 10; б) 73; в) 206; г) 
; д) 
;
е) 
. 2. а) (110110); б) (11111010000);
в) 
; г) при 
и 
; при 
; при 
. 3. а) (001)(101)(111); (010) (110)}; (101) (111); соседние: (001) и (101), (010) и (110), (101) и (100), (101) и (111), (110) и (111); противоположные (001) и (110), (010) и (101); б) (00110)(00111), (00110)(10110), (01010)(01011)(11011), (01010)(11010)(11011); шесть пар соседних наборов; противоположных наборов нет. 4. а) 
; б) 
;
в) 
; г) 
. Указание. Любой набор, отстоящий от фиксированного набора на расстоянии , получается из подходящей заменой некоторых компонент на противоположные. д) 
.
6. а) 
; б) 
; в) 2; г) 
.
7. а) 
; б) Нет. Указание. Предполагая, что 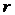, если член 
присутствует на заседании, и 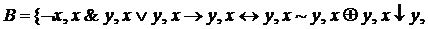, если отсутствует, условия задачи с помощью булевой функции можно представить в виде 
. 
и 
. Следовательно, также может не участвовать.
8. а) фиктивные переменные и ; б) фиктивная переменная ;
в) фиктивная переменная . 9. а) &, , , , , 
, 
, 
, , ; б) 218.