Эйлеровы пути. Эйлеровы циклы
В графе G путь из а в b называется эйлеровым путем, если он содержит все ребра графа, причем каждое по одному разу. Эйлеров цикл – путь из а в а, который содержит все ребра графа, каждое по одному разу.
Гамильтонов путь – путь, обходящий все вершины графа по одному разу. Гамильтонов цикл – путь из а в а, обходящий все вершины графа, кроме а, по одному разу.Теорема. Пусть дан связный граф. В нем существует эйлеров путь тогда и только тогда, когда две вершины графа имеют нечетную степень, а все остальные – четную. Эйлеров цикл существует тогда и только тогда, когда все вершины графа имеют четную степень.
 Доказательство. Доказательство обеих частей теоремы проведем одновременно.
Доказательство. Доказательство обеих частей теоремы проведем одновременно.
Необходимость. Пусть в графе G существует эйлеров путь из а в b. Тогда  – нечетное число. Действительно, из а выходит по крайней мере одно ребро, обозначим его е1 . Если путь возвращается в а по ребру е2, то он должен и выходить из него по ребру е3, и так далее (рис. 2.38,а). Степень вершины а – нечетная. Аналогично для вершины b. Если путь из а в а – эйлеров цикл, то первое и последнее ребро цикла инцидентны а. Если вершина а встречается внутри цикла, то вместе с ребром
– нечетное число. Действительно, из а выходит по крайней мере одно ребро, обозначим его е1 . Если путь возвращается в а по ребру е2, то он должен и выходить из него по ребру е3, и так далее (рис. 2.38,а). Степень вершины а – нечетная. Аналогично для вершины b. Если путь из а в а – эйлеров цикл, то первое и последнее ребро цикла инцидентны а. Если вершина а встречается внутри цикла, то вместе с ребром  он содержит и ребро
он содержит и ребро  . Степень вершины а – четная. Остальные вершины – внутренние и для эйлерова пути, и для эйлерова цикла, поэтому, если путь или цикл содержит ребро
. Степень вершины а – четная. Остальные вершины – внутренние и для эйлерова пути, и для эйлерова цикла, поэтому, если путь или цикл содержит ребро  , то он содержит и ребро
, то он содержит и ребро  , если
, если  .
.
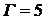 – четная (рис. 2.38,б).
– четная (рис. 2.38,б).  Достаточность. Доказательство проведем индукцией по количеству ребер. Пусть
Достаточность. Доказательство проведем индукцией по количеству ребер. Пусть  ,
,  – нечетные. Наименьшее количество ребер равно 1. При этом граф G состоит из двух вершин а и b и соединяющего их ребра, который и будет являться эйлеровым путем. Если степени всех вершин четные, то наименьшее количество ребер равно трем (при отсутствии кратных ребер). Если степени всех вершин четные, возможен только граф, изображенный на рис. 2.39. Эйлеров цикл существует. Предположим, для графа с количеством ребер, меньшим п, утверждение истинно. Докажем утверждение для графа с п ребрами. Удалим произвольное ребро, выходящее из а. Если удаление ребра нарушает связность, то удалим вместе с ребром и вершину а. Если удалено ребро (а,b), то степени всех вершин нового графа четны, граф связный, и по индукционному предположению, в нем существует эйлеров цикл. Его можно начинать из произвольной вершины. Для нового графа рассмотрим эйлеров цикл из b в b. Присоединив к нему ребро (а, b) (возможно вместе с вершиной а), получим эйлеров путь из b в а в исходном графе.
– нечетные. Наименьшее количество ребер равно 1. При этом граф G состоит из двух вершин а и b и соединяющего их ребра, который и будет являться эйлеровым путем. Если степени всех вершин четные, то наименьшее количество ребер равно трем (при отсутствии кратных ребер). Если степени всех вершин четные, возможен только граф, изображенный на рис. 2.39. Эйлеров цикл существует. Предположим, для графа с количеством ребер, меньшим п, утверждение истинно. Докажем утверждение для графа с п ребрами. Удалим произвольное ребро, выходящее из а. Если удаление ребра нарушает связность, то удалим вместе с ребром и вершину а. Если удалено ребро (а,b), то степени всех вершин нового графа четны, граф связный, и по индукционному предположению, в нем существует эйлеров цикл. Его можно начинать из произвольной вершины. Для нового графа рассмотрим эйлеров цикл из b в b. Присоединив к нему ребро (а, b) (возможно вместе с вершиной а), получим эйлеров путь из b в а в исходном графе.
Если произвольное ребро, выходящее из а, – это ребро (а, с),  , то, удалив его, получим, что степень вершины а стала четной, а степень вершины с – нечетной, число ребер уменьшилось на 1. Если удаление ребра нарушает связность, то удалим вместе с ребром и вершину а. В новом графе G' также две вершины с четными степенями (b и с), остальные – с нечетными степенями. По предположению индукции в G' существует эйлеров путь из с в b. Добавив к нему ребро (а, с), получим эйлеров путь из а в b.
, то, удалив его, получим, что степень вершины а стала четной, а степень вершины с – нечетной, число ребер уменьшилось на 1. Если удаление ребра нарушает связность, то удалим вместе с ребром и вершину а. В новом графе G' также две вершины с четными степенями (b и с), остальные – с нечетными степенями. По предположению индукции в G' существует эйлеров путь из с в b. Добавив к нему ребро (а, с), получим эйлеров путь из а в b.
Докажем теперь утверждение для эйлерова цикла с п ребрами. Пусть связный граф G имеет вершины только с четными степенями. Удалив из него одно ребро, например, (а, b) , получим граф G', у которого степени двух вершин нечетны, остальные – четны. Предположим, что удаление ребра нарушило связность графа, т.е. у графа G' две компоненты связности G1 и G2, при этом вершины с нечетными степенями а и b находятся в разных компонентах связности. Тогда сумма степеней вершин для каждого из графов G1 и G2 нечетна, чего не может быть. Следовательно, граф G' – связный, и по индукционному предположению в нем существует эйлеров путь из а в b. Добавив к эйлерову пути ребро (а, b), получим эйлеров цикл. Теорема доказана.