§1.6. Дизъюнктивные нормальные формы
Пример. Рассмотрим функцию 
. Приведем несколько различных формул, являющихся д. н. ф. и реализующих функцию 
.
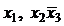и д. н. ф.: 
, 
, 
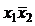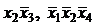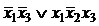. Заметим, что 
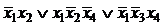. Лемма. Число различных д. н. ф. от переменных 
равно 
.
Доказательство. Действительно, число различных элементарных конъюнкций 
равно 
(“пустой” конъюнкции сопоставлена константа 1), так как для каждой переменной 
имеется три возможности: присутствует в конъюнкции, присутствует с отрицанием и отсутствует. Выпишем все элементарные конъюнкции, поставив между ними дизъюнкции: 
. Удаляя различные 
, получим все возможные д. н. ф. Следовательно, число различных д. н. ф. равно 
и одной функции соответствует несколько различных д. н. ф.
Введем функционал 
, означающий сложность д.
1. 
.
2. Если 
, то 
.
3. Если 
и 
, то 
.
4. Если 
и 
получены одна из другой переименованием переменных, то 
.
Примеры: 1) 
– число букв в д. н. ф.; 2) 
– число элементарных конъюнкций; 3) 
– число знаков отрицаний.
Тогда для рассмотренного в начале параграфа примера:
, 
, 
;
, 
;
, 
, 
.
Д. н. ф. называется минимальной для данной функции , если имеет минимальное значение.
Проблема минимизации д. н. ф. состоит в том, чтобы для произвольной функции построить минимальную д. н. ф. Конечно, существует алгоритм, реализующий проблему минимизации, – это алгоритм полного перебора. Однако, этот алгоритм занимает слишком много времени, и для функций, зависящих от большого числа переменных, реализован быть не может. В связи с этим важное значение приобретают методы, позволяющие за реальное время получить д. н. ф., в той или иной степени приближенные к минимальной.