2.1.5.Совершенные нормальные формы
 ,
,
где дизъюнкция берется по всем наборам с=(с1, с2, …, сn) из 0 и 1, для которых F(c)=1.
Теорема (о СДНФ). Для всякой не равной тождественному нулю формулы логики высказываний F(x1, x2, …, xn) существует такая формула F1, зависящая от того же списка переменных и находящаяся в СДНФ относительно этого списка, что F1 выражает собой формулу F. Формула F1 определена однозначно с точностью до перестановки дизъюнктивных членов.
Определение. Совершенной конъюнктивной формулой формулы алгебры высказываний (СКНФ) называется КНФ, в которой: различны все члены конъюнкции; различны все члены каждой дизъюнкции; ни одна дизъюнкция не содержит переменную вместе с отрицанием этой переменной; каждая дизъюнкция содержит все переменные, входящие в исходную формулу, т. е. имеет вид
 ,
,
где конъюнкция берется по всем наборам с=(с1, с2, …, сn) из 0 и 1, для которых F(c)=0.
Теорема (о СКНФ). Для всякой не равной тождественной единице формулы логики высказываний F(x1, x2, …, xn) существует такая формула F1, зависящая от того же списка переменных и находящаяся в СКНФ относительно этого списка, что F1 выражает собой формулу F. Формула F1 определена однозначно с точностью до перестановки конъюнктивных членов.
Опишем два способа приведения к совершенным нормальным формам.
1-й способ – аналитический.
Приведение к СДНФ. Алгоритм приведения. привести формулу с помощью равносильных преобразований к ДНФ.
удалить члены дизъюнкции, содержащие переменную вместе с ее отрицанием (если такие окажутся); из одинаковых членов дизъюнкции (если такие окажутся) удалить все, кроме одного; из одинаковых членов каждой конъюнкции (если такие окажутся) удалить все, кроме одного; если в какой-нибудь конъюнкции не содержится переменной xi из числа переменных, входящих в исходную формулу, добавить к этой конъюнкции член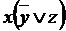 и применить закон дистрибутивности конъюнкции относительно дизъюнкции; если в полученной дизъюнкции окажутся одинаковые члены, воспользоваться предписанием из п. 3.
и применить закон дистрибутивности конъюнкции относительно дизъюнкции; если в полученной дизъюнкции окажутся одинаковые члены, воспользоваться предписанием из п. 3. Полученная формула и является СДНФ данной формулы.
Пример 27.
Привести следующие формулы к СДНФ с помощью равносильных преобразований:
1.  ;
;
2.  ;
;
3.  .
.
Решение.
1.  .
.
2. 
3. 
Приведение к СКНФ. Алгоритм приведения. привести формулу с помощью равносильных преобразований к КНФ. удалить члены конъюнкции, содержащие переменную вместе с ее отрицанием (если такие окажутся); из одинаковых членов конъюнкции (если такие окажутся) удалить все, кроме одного; из одинаковых членов каждой дизъюнкции (если такие окажутся) удалить все, кроме одного; если в какой-нибудь дизъюнкции не содержится переменной xi из числа переменных, входящих в исходную формулу, добавить к этой дизъюнкции член  и применить закон дистрибутивности дизъюнкции относительно конъюнкции; если в полученной конъюнкции окажутся одинаковые члены, воспользоваться предписанием из п.
и применить закон дистрибутивности дизъюнкции относительно конъюнкции; если в полученной конъюнкции окажутся одинаковые члены, воспользоваться предписанием из п.
Полученная формула и является СКНФ данной формулы.
Пример 28.
Привести следующие формулы к СКНФ с помощью равносильных преобразований:
1.  ;
;
2.  .
.
Решение.
1. 
2. 
2-й способ – табличный.
Составляем таблицу истинности для данной функции.
Приведение к СДНФ. Алгоритм приведения.
Строим таблицу значений формулы. Рассматриваем только те строки, в которых значение формулы равно единице. Каждой такой строке соответствует конъюнкция всех аргументов (без повторений). Причем, аргумент, принимающий значение 0, входит в нее с отрицанием, значение 1 – без отрицания. Наконец, образуем дизъюнкцию всех полученных конъюнкций.
Пример 29.
Построить СДНФ для данных формул логики высказываний.
1.  .
.
2. 
Решение.
1.  .
.
Строим таблицу истинности (табл. 13) для формулы F:
Таблица 13
| № | x | y | z |  |  |  |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 |
| 3 | 0 | 1 | 1 | 0 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 1 | 1 | 1 | 1 |
| 6 | 1 | 1 | 0 | 0 | 0 | 0 |
| 7 | 1 | 1 | 1 | 0 | 1 | 1 |
Рассматриваем только 4, 5 и 7 наборы, так как только на этих наборах формула принимает значение равное единице.
СДНФ имеет вид: 
2. 2. 
Строим таблицу истинности (табл. 14) для формулы F:
Таблица 14
| № | x | y | x® y | F=(x® y)ÙxÙy |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 2 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 1 | 1 |
СДНФ (1): № 3:
F = x y.
Приведение к СКНФ. Алгоритм приведения.
Рассматриваем только те строки таблицы, где формула принимает значение 0. Каждой такой строке соответствует дизъюнкция всех переменных (без повторений). Причем аргумент, принимающий значение 0, берется без отрицания, значение 1 – с отрицанием. Наконец, образуют конъюнкцию полученных дизъюнкций.
Пример 30.
Построить СКНФ для данных формул логики высказываний.
1.  .
.
2. 
Решение. Строим таблицу значений, используя предыдущий пример (табл. 15).
Таблица 15
| № | x | y | z |  |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 1 |
Рассматриваем только наборы, на которых формула принимает значение ноль.
СКНФ (0): № 0, 1, 2, 3, 6:
 Строим таблицу значений, используя предыдущий пример (табл. 16).
Строим таблицу значений, используя предыдущий пример (табл. 16).
Таблица 16
| № | x | y | F=(x® y)ÙxÙy |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 1 | 1 | 1 |
СКНФ (0): № 0, 1, 2:
