18. Общее понятие разностных уравнений
В качестве аналогов дифф.уров можно рассм. разностные ур-ния. При использовании обратных разностей линейные неоднородные разностные уравнения имеют вид: 
где f[n] –заданная, а y[n] –искомая решетчатые ф-ции.
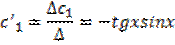уравнение становится однородным. Другой вид разн. ур-ния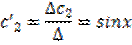 
Это разностное ур-ние можно рассматривать как рекуррентное отношение позволяющее вычислять значения y[n] для любых n по известному значению функции в правой части уравнения и начальным условиям y[n-1],…y[n-m]. Такие вычисления легко выполняются на счетных машинах, а также не представляют никаких принципиальных трудностей и при ручном счете, даже в тех случаях кошда коэффициенты в левой части уравнения меняются по времени. Это отличает разностные уравнения от непрерывных аналогов – дифф.уров.
Общее решение однородного разностного уравнения при некратных корнях характеристичесого уравнения может быть записано след.образом
где 
-корни характеристического уравнения 
а 
-произвольные постоянные.