16. Линейные неоднородные дифференциальные уравнения высших порядков. Метод вариации произвольной постоянной









Пример.














…

 17. Уравнение Эйлера
17. Уравнение Эйлера
 где все
где все  постоянные, называются уравнениями Эйлера.
постоянные, называются уравнениями Эйлера.
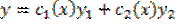 (t=lnx; y(x)=y(x(t)))преобразуется в линейное однородное уравнение с постоянными коэффициентами.
(t=lnx; y(x)=y(x(t)))преобразуется в линейное однородное уравнение с постоянными коэффициентами. Линейно входящие в ур-ние Эйл. с постоянными коэфф.произведения
с постоянными коэфф.произведения
 линейно выражаются через производные функции у по новой независимой переменной t. Отсюда => что преобразованное ур-ние будет линейным однородным ур-нием с постоянными коэффициентами.
линейно выражаются через производные функции у по новой независимой переменной t. Отсюда => что преобразованное ур-ние будет линейным однородным ур-нием с постоянными коэффициентами.
Пример. 











Если уравнение не однородное то переменную x на 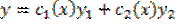 заменяют как в левой так и в правой частях.
заменяют как в левой так и в правой частях.
Если уравнение более высокого порядка, чем 2 то замена  на
на происходит по аналогичной схеме.
происходит по аналогичной схеме.
Еще по теме 16. Линейные неоднородные дифференциальные уравнения высших порядков. Метод вариации произвольной постоянной:
-
Аналитическая геометрия -
Вариационное исчисление -
Векторный и тензорный анализ -
Высшая геометрия -
Высшая математика -
Вычислительная математика -
Дискретная математика -
Дифференциальное и интегральное исчисление -
Дифференциальные уравнения -
Исследование операций -
История математики -
Комплексное исчисление -
Линейная алгебра -
Линейное программирование -
Математика для экономистов -
Математическая логика -
Математическая физика -
Математический анализ -
Пределы -
Ряды -
Статистика -
Теория вероятностей -
Теория графов -
Теория игр -
Теория принятия решений -
Теория случайных процессов -
Теория чисел -
Функциональный анализ -
-
Архитектура и строительство -
Безопасность жизнедеятельности -
Библиотечное дело -
Бизнес -
Биология -
Военные дисциплины -
География -
Геология -
Демография -
Диссертации России -
Естествознание -
Журналистика и СМИ -
Информатика, вычислительная техника и управление -
Искусствоведение -
История -
Культурология -
Литература -
Маркетинг -
Математика -
Медицина -
Менеджмент -
Педагогика -
Политология -
Право России -
Право України -
Промышленность -
Психология -
Реклама -
Религиоведение -
Социология -
Страхование -
Технические науки -
Учебный процесс -
Физика -
Философия -
Финансы -
Химия -
Художественные науки -
Экология -
Экономика -
Энергетика -
Юриспруденция -
Языкознание -