14. Линейные дифференциальные уравнения высших порядков
Лин.Диф.Ур-нием n порядка называется уравнение линейное относительно неизвестной функции и ее производных и, следовательно, имеющее вид:
(1)
Если правая часть 
, то уравнение называется линейным однородным, т.к.оно однородно относительно неизвестной ф-ии 
и ее производных.,иначе называется не однородным.
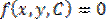то данное уравнение является нестационарным, а если 
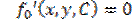то уравнение стационарное. Т1. Если 
есть решение диф.ура 
. То 
также является решением этого этого ур-ния. 
Т2. Если 
есть решение уравнения (1), то 
также явл.решением данного ур-ния.
Замечание: Если 2 решения можно определить как 
то такие решения называются линейно зависимыми. 
–линейно не зависимыми.
Т3.Если 
есть лин.зависимые решения ур-ния (1), то определитель Вронского =0.
Т4.
Если на каком либо отрезке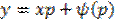
при начальных условиях 
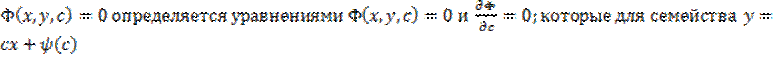и определитель Вронского в этой точке 
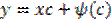, то во всех остальных точках отрезка опред-ль Вронского 
Т5. Если есть лин.независимые частные решения ур-ния (1), то общее решение этого уравнения можно представить в виде: 
.
1.это выражение явл-ся решением
2.это решение явл-ся общим решением.( 
)
15. Линейные неоднородные дифференциальные уравнения высших порядков. Метод
Подбора
Т.Общее решение лин.неоднородного ур-ния может быть представлено как сумма двух решений.
где
-общее решение, 
-к-либо частное решение неоднородн.ур-ния.
Пусть 
есть решения соответств. однородного ур-ния: 
(скобка =0).
;
- общее решение для любых началных условий
Метод подбора.
, 
если 
не есть корень характеристического ур-ния
(сокращаем на 
)
Если 
тогда 
=> 
Пример.
-общ.решение.
