2.Уравнения с разделяющимися переменными.

Дифференциальное уравнение I порядка называется уравнением с разделяющимися переменными, если его правая часть есть произведение функций, одна из которых зависит от переменной x , другая – от y: .

Уравнение, записанное в симметричной форме является уравнением с разделяющимися переменными, если множители и представляют собой произведение функций, из которых одна зависит только от переменной x , другая – от переменной y : .

Разделить переменные – значит преобразовать уравнение так, чтобы каждая переменная содержалась только в том слагаемом, которое содержит её дифференциал.

Для этого достаточно уравнение привести к форме

и умножить обе его части на функцию , в результате чего получится

.

Полученное равенство можно проинтегрировать:

Уравнение необходимо разделить почленно на выражение . Получаем равенство

,

которое можно проинтегрировать:

.

Вид уравнения:

Решение уравнения: приводим к уравнению с разделенными переменными () путем деления общих частей уравнения на (предполагая что ):

В частности, уравнение вида приводим к уравнению делением обеих частей на N(y):

Пример.

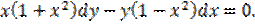
Решение: разделим обе части ур-ния на .

Потенцируя, найдем общее решение в виде